PID제어란?
산업 제어 시스템 및 다양한 자동 제어 분야에서 가장 널리 사용되는 피드백 제어 루프(Feedback Control Loop) 메커니즘
제어기의 세 가지 핵심 구성 요소인 비례(Proportional), 적분(Integral), 미분(Derivative) 항의 첫 글자를 딴 것
PID 제어의 각 요소
- P (비례, Proportional) 제어:
- 개념: 현재 시점의 오차 값에 비례하여 제어 출력을 결정. 오차가 크면 큰 제어 출력을 내고, 오차가 작으면 작은 제어 출력을 낸다.
- 수식 (간략화): P_out = Kp * e(t)
- Kp: 비례 이득 (Proportional Gain). 값이 클수록 오차에 대한 반응이 빨라지고 제어 강도가 커지지만, 너무 크면 시스템이 불안정해지거나 오버슈트(Overshoot, 목표값을 초과하는 현상)가 발생한다.
- 역할: 시스템의 현재 오차에 즉각적으로 반응하여 오차를 줄이려는 주된 제어 작용을 한다.
- 한계: 비례 제어만으로는 시스템에 외란(Disturbance)이 있거나 모델이 완벽하지 않을 경우, 목표값에 완전히 도달하지 못하고 일정한 오차(잔류 편차, Steady-state error 또는 Offset)가 남을 수 있다.
- I (적분, Integral) 제어:
- 개념: 과거부터 현재까지 누적된 오차의 합(적분값)에 비례하여 제어 출력을 결정한다.
- 수식 (간략화): I_out = Ki * ∫e(t) dt
- Ki: 적분 이득 (Integral Gain). 이 값이 클수록 잔류 편차를 더 빨리 제거하려 하지만, 너무 크면 시스템 응답이 느려지거나 진동을 유발하고 오버슈트가 커진다.
- 역할: 비례 제어만으로 제거하기 어려운 잔류 편차를 시간이 지남에 따라 점차 줄여 없애는 역할을 한다.
즉, 오차가 지속되면 적분항의 출력이 계속 커져서 결국 오차를 0으로 만든다. - 한계:
- 시스템의 응답을 느리게 만들 수 있다.
- 적분 와인드업(Integral Windup): 제어 출력이 이미 포화 상태(최대 또는 최소 한계에 도달)임에도 불구하고 오차가 계속 누적되어 적분항이 과도하게 커지는 현상. 이로 인해 시스템이 다시 정상 작동 범위로 돌아올 때 큰 오버슈트나 느린 회복을 보일 수 있다. (안티 와인드업 기법 필요)
- D (미분, Derivative) 제어:
- 개념: 현재 오차의 변화율(미분값), 즉 오차가 얼마나 빠르게 변하고 있는지에 비례하여 제어 출력을 결정한다. 미래의 오차를 예측하여 선제적으로 대응하는 효과가 있다.
- 수식 (간략화): D_out = Kd * de(t)/dt
- Kd: 미분 이득 (Derivative Gain). 이 값이 클수록 오차의 변화에 더 민감하게 반응하여 시스템의 안정성을 높이고 오버슈트를 줄이는 데 도움을 주지만, 너무 크면 측정값의 노이즈(Noise)에 과도하게 반응하여 시스템이 불안정해질 수 있다.
- 역할: 오차가 목표값에 빠르게 접근할 때 제어 출력을 줄여 오버슈트를 방지하고(댐핑 효과), 오차가 목표값에서 멀어지려고 할 때 제어 출력을 늘려 변화를 억제함으로써 시스템의 안정성을 향상시키고 응답 속도를 개선한다.
- 한계:
- 입력 신호의 갑작스러운 변화(예: 설정값의 급격한 변경)에 대해 매우 큰 미분값을 출력하여 시스템에 충격을 줄 수 있다.("미분 충격" 또는 "Derivative Kick". 이를 방지하기 위해 오차 대신 공정 변수의 변화율을 사용하기도 함)
- 측정값에 노이즈가 많을 경우, D항이 노이즈를 증폭시켜 제어 출력을 불안정하게 만들 수 있다. (필터링 필요)
PID 제어기의 전체 동작
세 가지 항의 출력을 합하여 최종 제어 출력을 결정.
MV(t) = P_out + I_out + D_out = Kp * e(t) + Ki * ∫e(t) dt + Kd * de(t)/dt
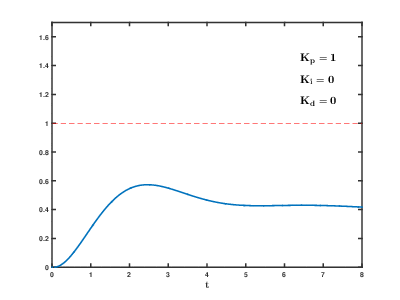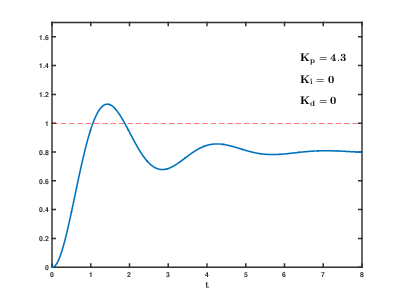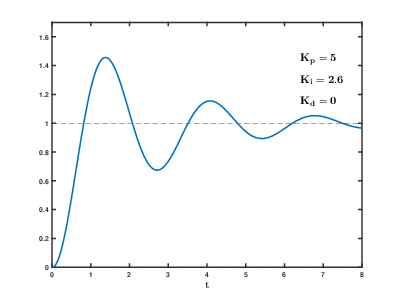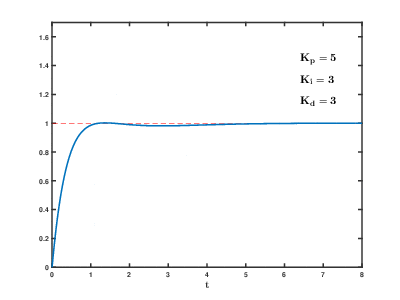
각 항은 시스템의 서로 다른 측면을 제어하며, 이 세 가지를 적절히 조합하고 각 이득(Gain) 값(Kp, Ki, Kd)을 시스템의 특성에 맞게 튜닝(Tuning)하는 것이 PID 제어 성능의 핵심.
원하는 응답 속도, 안정성, 정상 상태 오차 최소화 등 목적에 맞게 튜닝 값을 넣어주는게 핵심.
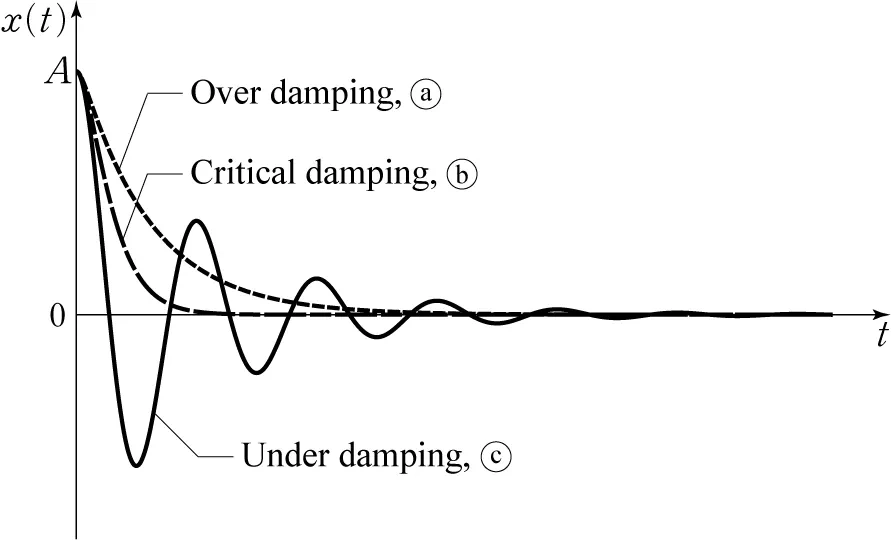

PID 각 요소에 대한 그래프는 다음 블로그를 참고 https://blog.naver.com/hitokirijinu/220961977414
P, PI, PD, PID 제어
PID 제어에 대해서. 회사에서 세미나 한것을 간단히 정리해본다. 일단 P : 비례제어 I : 적분제...
blog.naver.com
https://capitalists.tistory.com/239
PID 제어 방식의 이해 - 차속제어, 스티어링휠 제어
PID 제어 (PID control) (Proportional-Integral-Differential controller) (비례-적분-미분 제어기) 실제 응용분야에서 가장 많이 사용되는 대표적인 형태의 제어기법이다. 기본적으로 피드백(Feedback)제어기의 형태
capitalists.tistory.com
모델이 단순하기 때문에 다양한 분야에서 활용된다.
DC모터부터 산업 공정의 온도 압력 유량 농도 등 플랜트 설비부터, 로봇 팔의 모션, 속도제어, CNC 등 정밀제어에도 쓰이고, 차량의 크루즈 컨트롤, 자세제어, 드론이나 항공기의 자세, 고도 제어, 가전제품의 온도제어에도 쓰인다.
스티어링 비례제어
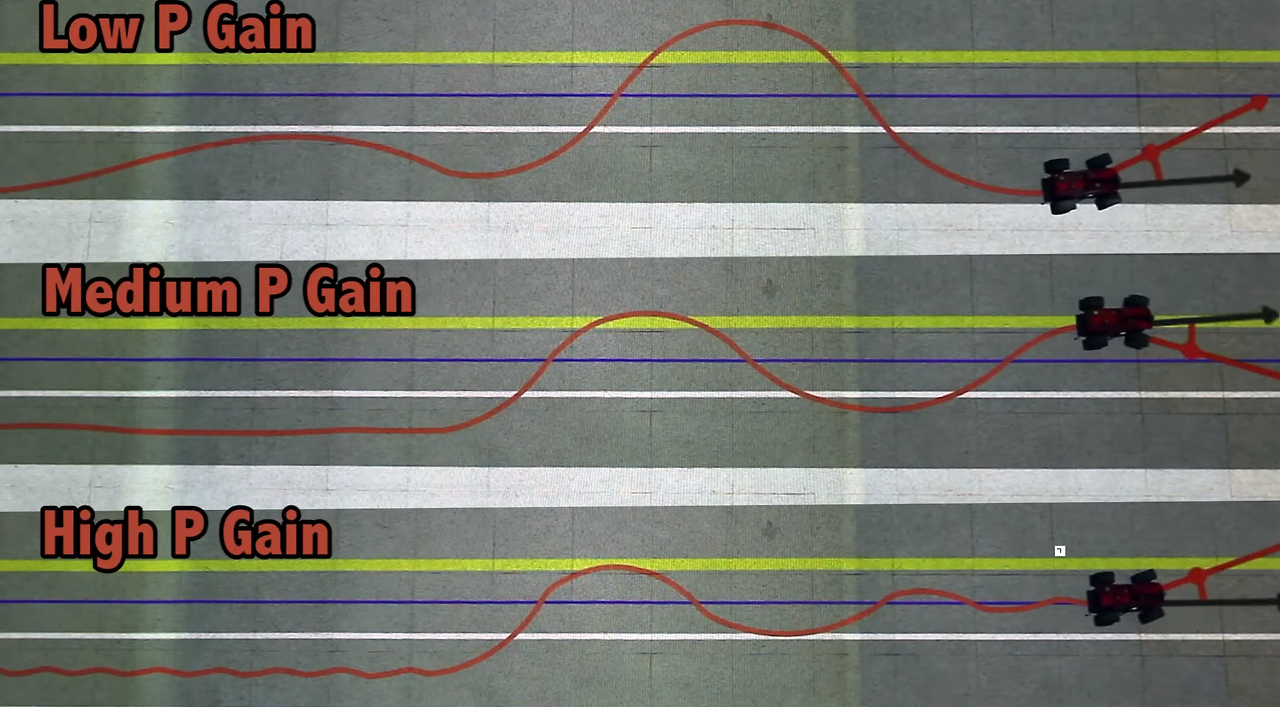
목표가 멀면 크게 꺾는다.
낮으면 너무 늦게 도달, 높으면 너무 덜덜거린다.
PD제어

낮은 D : 여전히 덜덜거린다. 높은 D: 도달에 너무 오래 걸린다.
P만으로는 오차가 0이 될 수 없다는 단점을 해결, 목표값에 도달하기 위해 시간이 오래 걸린다는 단점.
PID제어

낮은 I : 목표라인 도달이 오래 걸린다. 높은 I : 과반영으로 덜덜거린다.
언리얼에도 PID 컨트롤러를 응용한 기능이 있음.
https://code.vt.edu/shahwarak/drone-navigation-in-unreal-engine-using-a-pid
Shahwar Atiq Khursheed / Drone Navigation in Unreal Engine using a PID · GitLab
code.vt.edu
code.vt.edu
https://blueprintue.com/blueprint/hjwcptvo/
https://jacksgamedevblog.wordpress.com/2016/12/05/ue4-pid-controller-part-1-basic-cube/
UE4: PID Controller Part 1: Basic Cube
Introduction Another UE4 post but this time I thought I would actually create a code related one, as I am programmer after all haha. Again with like the previous posts I will not go in to much deta…
jacksgamedevblog.wordpress.com
https://www.fab.com/ko/listings/90cd917d-975b-482b-bc49-0243a6cea210
Plugins\Traffic\Source\MassTraffic\Public\MassTrafficPIDController.h
USTRUCT(BlueprintType)
struct MASSTRAFFIC_API FMassTrafficPIDController
{
GENERATED_BODY()
float Tick(float Goal, float Actual, float DeltaTime, const FMassTrafficPIDControllerParams& Params)
{
float Error = Goal - Actual;
if(Params.IntegralWindow > SMALL_NUMBER)
{
float WindowPortion = DeltaTime / Params.IntegralWindow;
ErrorIntegral *= (1.0f - WindowPortion);
ErrorIntegral += Error * WindowPortion;
}
else
{
ErrorIntegral = Error;
}
float Proportional = Params.ProportionalFactor * Error;
float Integral = Params.IntegralFactor * ErrorIntegral;
float Derivative = Params.DerivativeFactor * (Error - LastError);
LastError = Error;
return Proportional + Integral + Derivative;
}
void ResetErrorIntegral()
{
ErrorIntegral = 0.0f;
}
private:
UPROPERTY(Transient)
float ErrorIntegral = 0.0f;
UPROPERTY(Transient)
float LastError = 0.0f;
};
이해를 돕기 위해서는 일반물리, 공업수학, 진동학, 자동제어 지식이 필요함
조화진동, 발산, 감쇠진동 등의 키워드로 공부할 것을 추천함
'세미나' 카테고리의 다른 글
| 메모리 프로파일링, 최적화, GC (0) | 2025.05.14 |
|---|---|
| 2차 미분방정식의 물리적 예시 (0) | 2025.05.12 |
| 공업수학 복소해석학, 복소평면 (0) | 2025.05.12 |


